揭秘VAE背后的数学原理

背景

主要内容

• 背景
  • VAE在图像生成模型扮演了非常重要的角色
  • ELBO应用: VQVAE, Diffusion Model, Dalle
  • 数学门槛较高: 概率/泛函/微积分
• 生成模型之概率建模
  • 生成模型在做什么/如何对概率密度建模/挑战
• VAE建模之数学基础
  • 最大似然/蒙特卡洛/大数定律/维数灾难/积分变量替换/变分
• VAE
  • 基于隐变量的生成模型/优化的困难
  • 变分思想/下界的导出/如何求解
• VAE的代码实现
• 参考：
  • Tutorial on Variational Autoencoders (NO_ITEM_DATA:doerschTutorialVariationalAutoencoders2021)
  • Auto-Encoding Variational Bayes (NO_ITEM_DATA:kingmaAutoEncodingVariationalBayes2022a)

生成模型

机器学习的几个topic

• 监督学习：分类/回归
• 无监督学习: 概率密度估计

监督学习中的概率建模

• 基于特征来推断目标事件发生的概率 \(P(Y=1|X)=\sigma(f_{\theta}(X))\)
• ctr 里面： 基于用户和item的特征信息来推测用户点击item的概率
• NLP 中的相关性模型： 基于用户输入的query和doc特征来推测两者相关的概率
• 我们很少需要对样本特征的分布\(P(X)\) 直接建模

生成模型在做什么？

• 对样本\(X\) 的概率分布\(P(X)\) 做估计
  • 知道什么样的样本出现的概率高，什么样的样本出现的概率低
• \(X\) 是什么？原始的特征输入。
  • 文本：一句话
    • ✅ X=I have a lovely dog.
    • ❌ X=Lovely Dog have a i.
  • 图像: 灰度的图的话，一个矩阵 \(X=\begin{pmatrix} 1 & 2 & 3 \\ 5 & 7 & 9 \\ 200 & 222 & 255 \\ \end{pmatrix}\)

• 图像的例子

  ✅
  ❌

用概率的语言描述这个世界

• 我看到的都是一些实实在在的东西，一个图像怎么用概率来描述？
• 可以认为
  • 这个世界上的一切都是不确定的
  • 发生的事实背后都有一个对应的概率分布
  • 发生的事实其实都是上帝在基于这个分布采样的结果
• 比如：
  • P(用户点击广告|用户, 广告)
    • 基于用户和广告的特征，经过一个DNN输出了一个概率值P
    • 然后基于二项分布采样得到了最后的事实
• 一张图像，我们可以认为是采样的结果
  • 一张灰度图像可以看做是一个n*n维度的向量
  • 整体是一个gauss分布
  • 简单的可以认为是各向同性的，像素之间相互独立。

生成模型的目的

• 对图像的likelihood给出一个客观的判断
• 基于概率采样生成
  • 我们可以生成更多的类似的，不在样本集合中的 X
• 例子：
  • 给一些树木的样例图片，可以生成一片森林出来。
  • conditional 的时候会产生更大的价值
    • 控制的图像生成，P(x|c), 文本到图像的生成

• 例子1

  

• 例子2

  

概率密度建模

概率密度建模的难点在哪里？

建模密度函数\(P_{\theta}(x)\)

• 约束

  • \(P_{\theta}(x)\ge 0, \forall x \in \mathcal{X}\)
  • \(\int P_{\theta}(x) dx=1, \forall \theta \in \Theta\) ✅ 真正的难点

• \(\nabla_{\theta} log P_{\theta}(x)\) 是否容易计算

  • \(P(x)=\int P(x,z) dz\) ❌

• 能够容易sample 采样生成

  • autogressive model 应用在图像像素级别 ❌

限定概率分布的形状，对pdf参数做函数化

• 假设这个分布是 \(\mathcal{N}(\mu_{\theta}(x),\Sigma_{\theta}(x))\)
• 极大似然估计来推断 \(\mu_{\theta}, \Sigma_{\theta}\)
• 这个方法在VAE中大量的出现，比如对\(Q_{\phi}(Z|X), P_{\theta}(Z|X)\)

限定序列结构做条件概率展开

• 依赖：
  • \(X\) 是可以序列化的 \(X=(x_{1}, x_{2},\ldots, x_{n})\)
  • \(P(x_{1}, x_{2},\ldots, x_{n})= P(x_{1})P(x_{2}|x_{1})\ldotsP(x_{n}|x_{1,\ldots,n-1})\)
• 对中间的每个条件概率项做好归一化即可

  • \(\int P(x_i|x_{1,\ldots,i-1}) dx_i=1\)

  • \(\int P(x_{1}, x_{2},\ldots, x_{n}) dx_1dx_2\cdots dx_n=1\)

  • 在DNN中，表现为最后一层做softmax

    比如dnn的language model 在训练的时候，为了输出token \(x_{i}\) 的概率，需要对所有的token做一个打分, 然后softmax

• autoregressive models
• 例子：
  • language model
  • image model: pixelRNN
    • 效率的问题: 1920*1080=207,3600
    • 如何序列化？

其他方法：

• 基于隐变量的生成模型
  • VAE
  • diffusion model
• GAN：其实绕开了对于概率密度的数学建模
• flow based

数学基础回顾

关于最大似然估计

什么是最大似然

• 数据集合 \(\mathcal{X}=\{X_1, X_2, \cdots, X_N}\}\)
• 建模 \(P_{\theta}(\mathcal{X})=\prod_{i}P(X_{i})\)
• 寻找参数\(\theta\)，使得\(\mathcal{X}\) 发生的概率 \(P_{\theta}(\mathcal{X})\) 最大化

理解

• 事实为依据，存在即合理
• 用模型来解释已经发生的事实 \(P(\mathcal{X}|\theta)\)
• 哪个模型输出的概率高，就用哪个
  • model1 预测 \(X\) 概率0.9
  • model2 预测 \(X\) 概率0.2
  • 而\(X\) 已经发生，选择和事实最接近的。

最大似然会有什么问题？

• 当数据量少的时候，会发生过拟合。

  • 发生的事实可能有噪音, 你的结论可能是拟合了噪音。

  • 类比地域歧视：

    你雇过两个阿姨，打扫卫生都不干净，你发现他们都来自于A 省份，然后你得出一个结论：A省份的阿姨打扫卫生都很差，以后坚决不找A省份的阿姨。

  • 不要因为一两次次失败就否定自己, 你的否定很可能是过拟合了。 :)

• 怎么办？
  • 读万卷书，先验的知识来纠偏, 贝叶斯的方法 \(P(\theta|\mathcal{X})=\dfrac{P(\mathcal{X}|\theta)P(\theta)}{P(\mathcal{X})}\)
  • 行万里路，看更多的数据，调整你的\(\theta\)
    • 但是人生短暂，实践的代价可能会很大 :)

蒙特卡洛方法和维度灾难

什么是MC

The underlying concept is to use randomness to solve problems that might be deterministic in principle.

计算期望

\(E_{X\sim p(x)} f(X)\)

• i.i.d sample \(\{X_{i}\}_{i=1}^{n} \sim p(x)\)
• \(\dfrac{1}{n}\sum_{i=1}^{n}f(X_{i})\rightarrow \mathrm{E}(f(X))\)

背后的依据：大数定律

• 如果\(\{X_i\}_{i=1}^{n}\) 独立同分布，那么 \(\dfrac{1}{n}\sum_{i=1}^{n}X_{i}\rightarrow \mathrm{E}(X)\)

• 应用到上面：

  如果\(\{X_i\}_{i=1}^{n}\) 独立同部分, 那么 \(\{f(X_i)\}_{i=1}^{n}\) 也是独立同分布的， 且\(\dfrac{1}{n}\sum_{i=1}^{n}f(X_{i})\rightarrow \mathrm{E}(f(X))\)

缺点：在高维空间中效率非常的低

• 在高维空间里面，你的采样到的大部分的点都不是你想要的

• 看一个面试题目：计算\(\pi\)

  • 在二维空间的解法
    • sample n个[-1,1] 之间的均匀随机变量
    • 计算落入半径为1的圆形中间的比例
    • \(\pi r^2/4r^{2}=\pi/4\)
  • 推广到n维空间中
    • \(n\) 维的球体的体积, 半径为\(R\)
    • \(V_n=\dfrac{\pi^{\frac{n}{2}}R^{n}}{\Gamma(\frac{n}{2}+1)},~\Gamma(n+1)=n!\)
    • 基于单位球体的体积公式反向推导 \(\begin{aligned}\pi &=(\dfrac{V_n\Gamma(\frac{n}{2}+1)}{R^n})^{\frac{2}{n}}\\ &=(\dfrac{V_n}{(2R)^{n}} \times 2^{n}\times \Gamma(\frac{n}{2}+1))^{\frac{2}{n}}\\ &=(\dfrac{V_{n}}{V_{cube}} \times 2^{n}\times \Gamma(\frac{n}{2}+1))^{\frac{2}{n}} \end{aligned}\)
    • 方法：
      • sample n个[-1,1] 之间的均匀随机变量
      • 计算单位球中的个数比例得到 \(V_{n}/V_{cube}\)
  • 维度灾难
    • \(V_{n}\rightarrow 0, n\rightarrow \infty\)
    • n维单位球体的体积趋向于0
    • sample失效

注：

• MC 偏好期望形式的优化目标 \(E_{P(X)} f(X)\)
• 例子：
  • \(E_{\tau\sim p(\tau)}r(\tau)\)
  • \(\int_{p(z|x)}p(x|z)dz\)

概率论基础的公式

链式法则

\(P(A_1 \cap A_2 \cap \ldots \cap A_n) = P(A_1) \times P(A_2 \mid A_1) \times \ldots P(A_n \mid A_1 \cap \ldots \cap A_{n-1})\)

• \(P(X_{1}X_{2}\ldots X_n) = P(X_1)P(X_2|X_1)\ldots P(X_{n}|X_{<n}})\)

贝叶斯公式

\(P(Z|X)=\dfrac{P(X|Z)P(Z)}{P(X)}\)

• \(P(Z)\) 先验
• \(P(X|Z)\) 似然性
• \(P(Z|X)\) 后验
• 在VAE中，\(Z\) 是隐变量，\(X\) 是图像
• 贝叶斯估计MAP，\(P(\theta|\mathcal{X}) = \dfrac{P(\mathcal{X}|\theta)P(\theta)}{P(\mathcal{X})}\)

高斯分布

定义

• \(X\sim \mathcal{N}(\mu,\Sigma)\)
  • 一维：\(X\sim \mathcal{N}(\mu, \sigma^{2})\) , \(p(x)=\dfrac{1}{\sqrt{2\pi\sigma^{2}}}\mathrm{exp}({-\dfrac{1}{2}(\dfrac{x-\mu}{\sigma})^{2}})\)
  • k维: \(p(x)=\dfrac{1}{\sqrt{(2\pi)^{k}|\Sigma|}}\mathrm{exp}(-\dfrac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\)
• mean vector: \(\mu=\mathrm{E}[X]\)
• covariance matrix:
  • \(\Sigma_{i,j} = \mathrm{E}[(X_i-\mu_i)(X_{j}-\mu_j)}]\)
  • 在VAE/diffusion model中，出现的都是对角矩阵 \(\Sigma=\sigma^{2}I\)

封闭性

• Affine transformation: if p(x) is Gaussian, then p(Ax + b) is a Gaussian.
• 高斯随机变量的线性组合还是高斯分布
  • VDM: \(z_{t}=\sqrt{1-\beta_t}{z_{t-1}}+\beta_{t}\varepsilon\)
• Product: if p(x) and p(z) are Gaussian, then p(x)p(z) is proportional to a Gaussian
  • 先验高斯，似然高斯，后验依然是高斯
  • \(P(X|Z)=\dfrac{P(Z|X)P(X)}{P(Z)}\)
  • VDM：\(P(z_{t-1})\) 高斯，\(P(z_t|z_{t-1})\) 高斯，那么\(P(z_{t-1}|z_{t})\) 也是高斯。
• Marginalization: if p(x, z) is Gaussian, then p(x) is Gaussian.
• Conditioning: if p(x, z) is Gaussian, then p(x | z) is Gaussian.

KL divergence

• 两个高斯分布之间的KL divergence \(\begin{aligned} &\mathcal{D}\left[ \mathcal{N}(\mu_0, \Sigma_0) \parallel \mathcal{N}(\mu_1, \Sigma_1) \right] \\ =& \frac{1}{2} \left( \text{tr} \left( \Sigma_1^{-1}\Sigma_0 \right) + (\mu_1 - \mu_0)^T \Sigma_1^{-1} (\mu_1 - \mu_0) - k + \log \left( \dfrac{\det\Sigma_1}{\det\Sigma_0} \right) \right) \\ \end{aligned}\)
• VAE中的涉及：后验和先验之间的距离 \(\begin{aligned} & \mathcal{D}\left[P(Z|X) \parallel P(Z)\right] \\ =&\mathcal{D}\left[ \mathcal{N}(\mu(X), \Sigma(X)) \parallel \mathcal{N}(0, I) \right] \\ =& \frac{1}{2} \left( \text{tr}(\Sigma(X)) + (\mu(X))^T (\mu(X)) - k - \log \det (\Sigma(X)) \right) \end{aligned}\)

重参数化

问题：

• 两种情形下求梯度
  • \(\nabla_{\theta}\mathrm{E}_{p(z)} \left[ f_\theta(z) \right]\)，pdf没有参数
  • \(\nabla_{\theta}\mathrm{E}_{p_{\theta}(z)} \left[ f_\theta(z) \right]\)，pdf有参数
• VAE: reconstruction error 的梯度计算
  • \(\nabla_{\phi}E_{Q_{\phi}(Z|X)}\log P_{\theta}(X|Z)\)

pdf不含有参数

\[ \nabla_\theta \mathrm{E}_{p(z)} \left[ f_\theta(z) \right] = \nabla_\theta \int p(z)f_\theta(z)dz \] \[ = \int p(z) \nabla_\theta f_\theta(z) dz \] \[ = \mathrm{E}_{p(z)} \left[ \nabla_\theta f_\theta(z) \right] \] 求导穿过了期望，这个好处在于可以对最后这个式子做MC

pdf中含有参数

\[ \nabla_\theta \mathrm{E}_{p_\theta(z)} \left[ f_\theta(z) \right] = \nabla_\theta \int p_\theta(z)f_\theta(z)dz \] \[ = \int \nabla_\theta \left[ p_\theta(z)f_\theta(z) \right] dz \] \[ = \int f_\theta(z) \nabla_\theta p_\theta(z) dz + \int p_\theta(z) \nabla_\theta f_\theta(z) dz \] \[ = \int f_\theta(z) \nabla_\theta p_\theta(z) dz + \mathrm{E}_{p_\theta(z)} \left[ \nabla_\theta f_\theta(z) \right] \]

• 多出来一个左端项，不好处理
• 进一步，如果我们基于MC来表达期望的话

重参数化=积分的变量替换

• 什么是reparameterization trick?

  • 如果 \(z\sim p_z, z = g(\varepsilon), \varepsilon \sim p_\varepsilon\)
  • 那么 \(\mathrm{E}_{p_{z}}f(z)=\mathrm{E}_{p_\varepsilon}f(g(\varepsilon))\)

• 应用

  如果期望依赖的pdf中有参数，而我们需要针对这个期望对参数求导 \(\begin{aligned} \nabla_\theta \mathrm{E}_{p_\theta(z)}[f(z)] &= \nabla_\theta \mathrm{E}_{p(\varepsilon)}[f(g_\theta(\varepsilon}))] \\ &= \mathrm{E}_{p(\varepsilon)}[\nabla_\theta f(g_\theta(\varepsilon}))] \\ &\approx \frac{1}{L} \sum_{l=1}^L \nabla_\theta f(g_\theta(\varepsilon^{(l)})) \end{aligned}\)

• proof:

  • 首先，两个pdf之间满足 \(p_\varepsilon=p_z(g(\varepsilon))g’(\varepsilon)\) \(\begin{aligned}P(\varepsilon < y) &= P(g^{-1}(z)<y) \\ &= P(z < g(y)) \\ & = \int_{-\infty}^{g(y)} p_z(s) ds \\ & \overset{s=g(\varepsilon)}{=} \int_{-\infty}^{y} p_z(g(\varepsilon))g’(\varepsilon) d\varepsilon \end{aligned}\)
  • 其次 \(\begin{aligned} & \quad\mathrm{E}_{p_{z}}f(z)\\ =&\int f(s)p_z(s) ds \\ \overset{s=g(\varepsilon)}{=}&\int f(g(\varepsilon))p_z(g(\varepsilon))g’(\varepsilon) d\varepsilon \\ =&\int f(g(\varepsilon))p_{\varepsilon}(\varepsilon)d\varepsilon \\ =& \mathrm{E}_{p_\varepsilon}f(g(\varepsilon)) \\ \end{aligned}\)

类比log trick

可以类比于强化学习中的 policy gradient 求导 \(J(\theta)= E_{\tau\sim \pi_{\theta}(\tau)} r(\tau)\)

\(\begin{aligned} \nabla_{\theta}J(\theta) = & \nabla_{\theta} \int\pi_{\theta}(\tau)r(\tau)d\tau \\ = & \int \nabla_{\theta}\pi_{\theta}(\tau)r(\tau)d\tau \\ = & \int \pi_{\theta}(\tau) \nabla_{\theta}\log \pi_{\theta}(\tau)r(\tau)d\tau \\ = & E_{\tau \sim \pi_{\theta}(\tau)}\left[ \nabla_{\theta}\log \pi_{\theta}(\tau)r(\tau) \right] \end{aligned}\)

启发：

1. 目标函数是一个期望的形式, 依赖的pdf中含有参数
2. 两种处理的手段
   • 重参数化
   • log trick

Jensen’s inequality

statement：

the secant line of a convex function lies above the graph of the function. \(f(tx_1+(1-t)x_{2}) \le tf(x_1)+(1-t)f(x_2), \forall t \in [0,1]\)

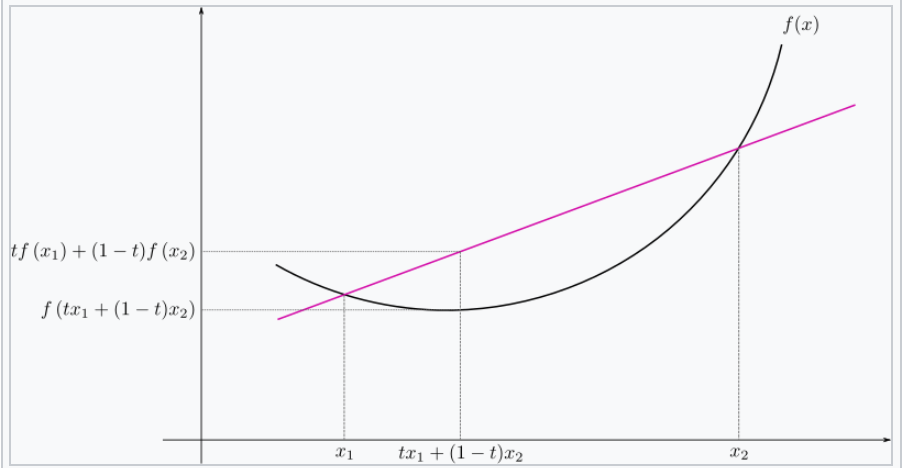
概率中的表述：

如果 \(X\) 是随机变量，\(f\) 是一个凸函数的话，\(f (E(X)) \le E(f(X))\)

注

• log函数是一个凹函数, \(\log (E(X)) \ge E(\log(X))\)
• 如果遇到 log和期望的时候，我们可以让log穿过期望符号，得到一个好的下界
  • VAE: \(\log E_{Q(Z)} \dfrac{P(X,Z)}{Q(Z)} dZ \ge E_{Q(Z)}\log\dfrac{P(X,Z)}{Q(Z)}\)

变分

泛函 fuctional

• 泛函是一个函数：
  • 输入是一个函数
  • 输出一个值
• 例如熵的定义：\(H(p)=\int p(x) \log p(x)dx\)
• 变分：是在一个函数空间中针对一个泛函来寻求极值。

DNN 求解是在做泛函极小化的事情

• 给定数据集合 \(D=\{(x_i,y_i)|i=1,\ldots, N\}\)

• loss：就是一个泛函

  \(J(f) = \sum\limits_{(x_i,y_i)\in D} L(f(x_i), y_i)\)

• 在函数空间\(F\) 中做泛函的极小, F是连续函数的空间，无穷维。 \(\min\limits_{f\in F} J(f)\)

• 参数化: 泛函极小化到参数极小化

  • 选定参数空间是DNN形式的函数
  • \(f(x)=f_{n}\circ \ldots f_1(x)}\), \(f_{i}\) 是一层DNN变换，\(\theta\) 是全部的DNN参数
  • \(f(x)=f_{\theta}(x)\)
  • \(\min\limits_{\theta} J(\theta)\) 有限维空间中求解

变分的感觉

• 有一个泛函的存在，\(J(f)\)
• \(f\) 在一个函数空间中变化 \(\mathcal{F}\)
• 对 \(J\) 求极值

• VAE中的变分

  \(\begin{aligned} \log P(X) & = \log \int P(X,Z)dZ \\ & = \log \int \dfrac{P(X,Z)}{Q(Z)} Q(Z) dZ \\ &= \log E_{Q(Z)} \dfrac{P(X,Z)}{Q(Z)} \\ &\ge E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)} \end{aligned}\)

  • 上面的式子对任意的概率分布\(Q(Z)\) 都成立
  • 泛函 \(\mathcal{L}(Q) = E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)}\)
  • 函数的空间是所有的PDF \(Q(Z)\)
  • 下界极大化

• 这个不是在做变分

  \(\begin{aligned} \log P(X) & = \log \int P(X,Z)dZ \\ & = log \int P(X|Z) P(Z) dZ \\ &= log E_{P(Z)} P(X|Z) \\ & \ge E_{P(Z)} \log P(X|Z) \end{aligned}\)

基于隐变量的生成模型

latent variables

什么是latent variables

• 我们看到的世界可能是高维空间到低维子空间的一个投影
• 我们观察获取到的信息\(X\) 本身是不完整的
  • 或者说，我们无法观测到完整的信息，盲人摸象
  • 例子：ctr预估，天气，人的心情，或者平台获取不到信息等
• 我们可以把观测之外的这些特征可以记作 latent variables

• Plato’s Cave

  In Plato’s allegory, a group of prisoners face the wall as a punishment and there are some physical objects behind them which the prisoners cannot see – the prisoners can only see the shadows of these objects on the wall. The shadows are otherwise the “observations” which the prisoners make – the observed variables. The physical objects are the “latent variables” the underlying variables governing the actual behaviour which we cannot directly see in Plato’s cave example.

  

图片的latent variable

• 尽管说，一张图片包含了所有的信息，但是很多的信息是你的人脑反馈分析出来的。
  • 比如这个图里面，你会反应出来它有簇，群的概念，这些就是\(Z\)

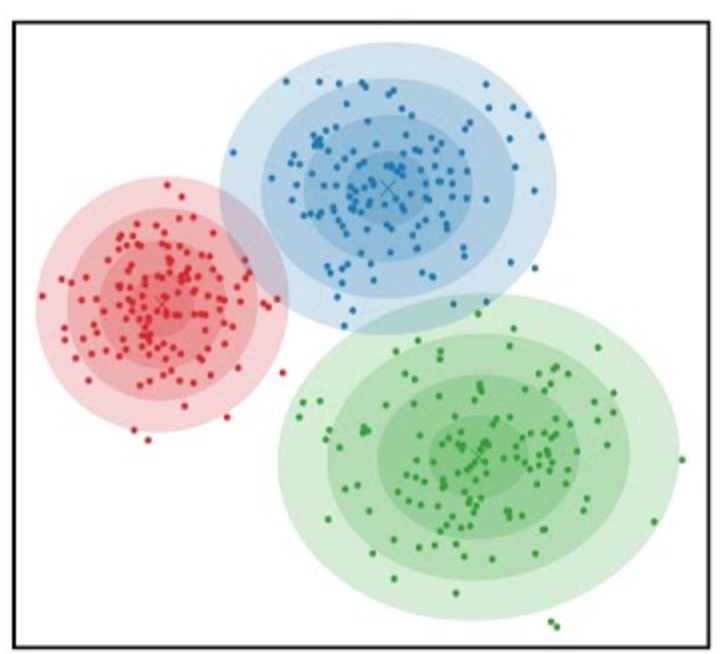
• 在人脸的图片中，\(Z\) 可能是肤色，脸型，发型，眼睛，鼻子的形状等

对的latent variables的一些假设

• 完整的样本是\((X, Z)\)
  • 每个样本\(X\) 对应一个latent variable \(Z\)
• 但是我们只能观测到\(X\), \(Z\) 是观测不到的, 且一般没有一个明确的定义
  • VAE中的\(Z\) 我们也不知道是feature，只是一种感觉
• 直接去优化 \(P_{\theta}(X)\) 是困难的, 有积分的存在
  • \(P(X)=\int_Z P_{\theta}(X,Z)dZ=\int_{Z}P_{\theta}(X|Z)P_{\theta}(Z)dZ\)
• 但是知道了\(Z\) 后，\(P(X,Z)\) 或者 \(P(X|Z)\) 是容易优化的

基于隐变量的生成模型

• latent variable 变的至关重要
  • \(Z\rightarrow X\)
  • \(Z\) 表达了图像中至关重要的特征
  • 知道了\(Z\), 整个图像就可以基于\(P(X|Z)\) decode 构建出来。
  • 我们会把 \(Z\) 当做是 $X$对一个的encoding 向量。
• 生成：观测值是基于隐变量的值来生成的。
  • 先sample \(Z\)
  • 再基于 \(P(X|Z)\) sample得到 \(X\)
• \(P(X,Z)=P(Z)P(X|Z)\)

一个例子：高斯混合模型

\(P(X)=\sum_{Z}P(Z)P(X|Z)=\sum\limits_{k=1}^{K} \pi_{k}\mathcal{N}(x|\mu_{k},\Sigma_{k})\)

• sample过程
  • 先根据先验\(P(Z)\) 决定在哪个群落点，
  • 再根据局部的似然 \(P(X|Z)\) 采样，(根据这个群的均值，方差采样)
• 直接优化 \(\log P(X)\) 非常困难
• 但是 \(P(X,Z)=\prod\limits_{k=1}^K \pi_k^{Z_k}\mathcal{N}(X|\mu_{k}, \Sigma_{k})^{Z_k}\),
  • 其中 \(Z=(Z_1, Z_2, \ldots, Z_{k})\) one-hot 形式
  • \(\log P(X,Z)=\sum\limits_{k=1}^{K}Z_k[log\pi_k+\log\mathcal{N}(X|\mu_{k}, \Sigma_{k})]\) 容易优化

• VAE 就是一个高斯混合模型

  • 假设 \(Z \sim \mathcal{N}(0, I)\)
  • 假设 \(P(X|Z) \sim \mathcal{N}(\mu(X), \Sigma(X))\)
  • \(P(X)=\int P(X|Z)P(Z) dX\)
    • 无穷个高斯的混合

基于隐变量的图像生成模型

不是把所有的图像放在一起做一个分布 \(P(X)\)

• 这样的分布有了可能用处也不大，你在高维sample的时候困难极其的大
• 另外你对sample做不了太多的控制

每个图像可以看做对应一个分布

• 每个图像都可以看做是一个高斯分布下的采样
• 按照像素点的当前值，是一个高斯分布，有均值，方差
• 如果我们把方差relax以下，我们也可以基于每个图像得到一些新的图像

从一图一个分布到一个编码一个分布

• 一个图像一个分布有点太细了，没法泛化
• 对图像\(X\) 来做低维编码\(Z\) ，如果编码相同，那么对应的分布是\(P(X|Z)\) 是相同的。
• 这套编码至关重要，有了它，图像的基本特征就决定了，
  • 人脸中，它可能包括了性别，肤色，发型，脸型等等
• 把这个编码空间学好了，你可以对生成的东西做更好的操控
• 如果把 \(P(X|Z)\) 学好了
  • 那么我直接采样 \(Z\) 就好了，
  • 这个分布需要很容易sample，首选的还是多维的gaussian 分布

隐变量生成模型的概率建模

一般的模型的概率建模方式

• 参数化单个样本\(X\) 的概率
  • \(P_{\theta}(X)\)
  • \(\log P_{\theta}(X)\) is easy
• 最大似然估计 \(\sum_{i} \log P_{\theta}(X_i)\)

生成式模型的概率建模方式

• 参数化单个样本
  • \(P_{\theta}(X)=\int P_{\theta}(X|Z)P_{\theta}(Z)dZ\)
• VAE:
  • \(P_{\theta}(X|Z)=\mathcal{N}(\mu(Z;\theta),\Sigma(Z;\theta))\)
  • \(P_{\theta}(Z)=\mathcal{N}(0,I)\)
• \(\log P_{\theta}(X)=\log \int P_{\theta}(X|Z)P_{\theta}(Z)dZ\) ???

生成式模型的概率建模本质

• 无穷个高斯模型的混合
• 每个图像\(X\)，都有一个对应\(Z\) 编码, 再对应一个该图像的分布
• sample:
  1. ancestral sample：\(Z\rightarrow X\)
  2. VDM \(Z_n\rightarrow Z_{n-1} \rightarrow Z_{n-2} \ldots \rightarrow X\)

隐变量生成模型的优化困难

优化的目标：

• \(P(X)=\int_Z P_{\theta}(X|Z)P(Z) dZ\)
• 积分的存在，导致 \(\log P(X)\) 无法直接优化

使用蒙特卡洛方法？

对于一个给定的样本 \(X\)

• 写成期望的形式 \(P(X)= E\limits_{Z\sim P(Z)} P_{\theta}(X|Z)\)
• MC
  • sample \(Z_1, Z_2, \ldots, Z_n\) from \(P(Z)\)
  • \(P(X) \approx \dfrac{1}{n} \sum_{i} P_{\theta}(X|Z_i)\)
  • 再针对\(\theta\) 做梯度下降

困难

• 维度灾难的问题：高维空间中的sample 效率很低。
• \(Z_{i}\) 的有效性
  • 直接来sample \(Z_{i} \sim P(Z)\)，\(P(X|Z_i)\) 的概率大多为0，可能导致模型一直 error很大，很难拟合样本。
  • 所以我们要更加有效的 Z, 最好使用 \(P(Z|X)\) 来sample \(Z\)
  • 但是 \(P(Z|X)\) 是未知的，找 \(Q(Z|X)\) 来近似 $P(Z|X)
  • 计算 \(E_{Z\sim Q} P(X|Z)\)

• \(\log P(X)\) 的问题

隐变量生成模型的另一个挑战

• 我们的初衷：\(Z\rightarrow X\)
  • 先sample \(Z\sim P(Z)\)
  • 再sample \(X\sim P(X|Z)\)
• \(Z\) 所在的 latent space 应该满足
  • 连续性：\(Z\) 连续变化的时候，生成的图像也是在连续变化的。
  • 完备性: 任意的一个sample \(Z\), 都可以被解码生成一个有意义的图像。

关于完备性：

本质是encoding部分\(Q(Z|X)\) 需要和你将来要sample的 \(P(Z)\) 之间是契合兼容的。

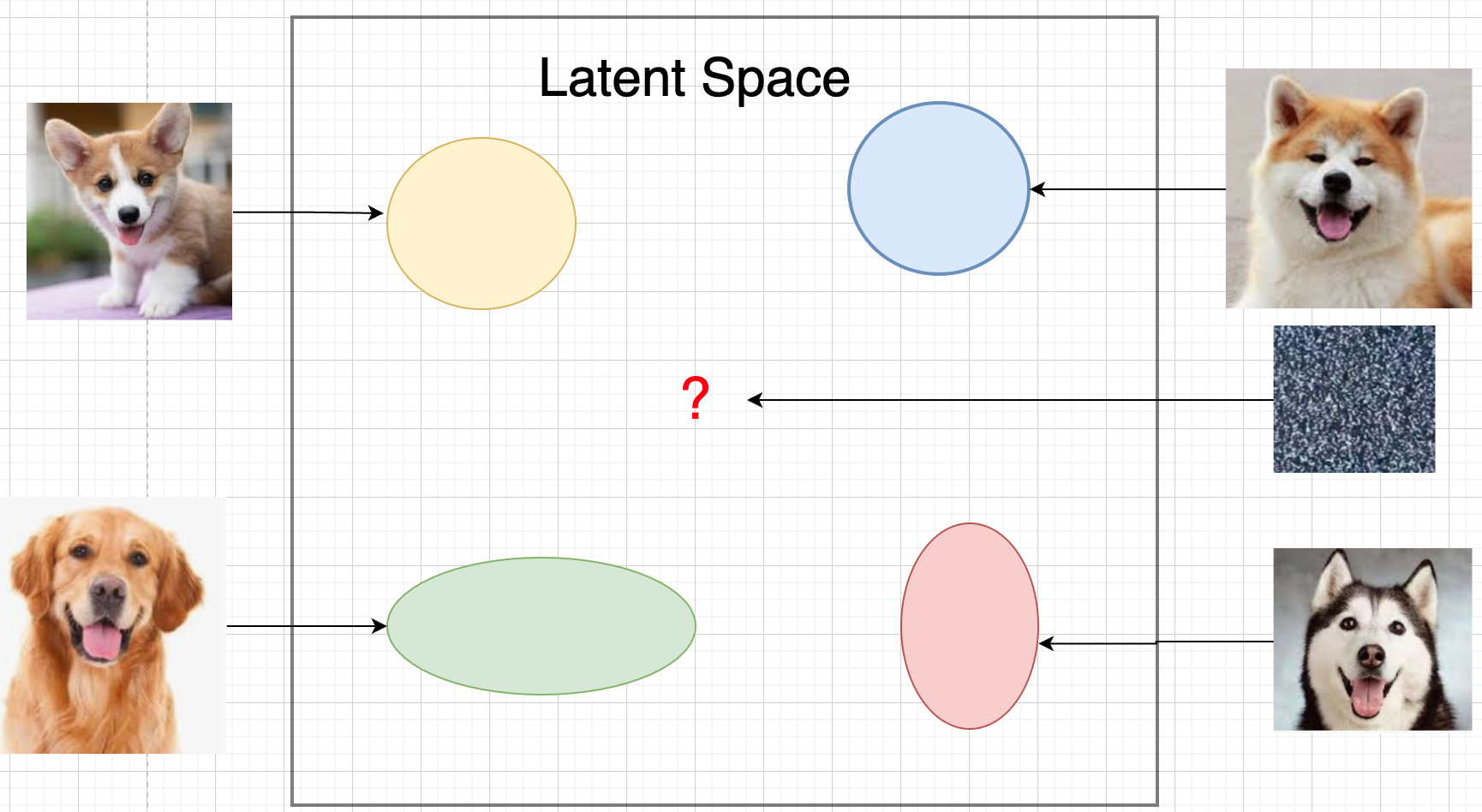
VAE

VAE 的思路

\(\log P(X)= \log \int P(X,Z) dZ\)

思考点一：log穿过积分

• 基于Jensen 不等式，\(\log\) 可以穿过去积分, 得到一个下界
  • 积分项中加入分布Q(Z)
  • 积分变成了期望，log穿过期望
• 而这个下界是容易优化的， 同时可以对下界优化不断提升

\(\begin{aligned} \log P(X) &= \log \int P(X, Z) dZ\\ &= \log \int P(X, Z) \dfrac{Q(Z)}{Q(Z)}dZ\\ &= \log E_{Q(Z)} \dfrac{P(X,Z)}{Q(Z)}\\ &\ge E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)}\\ \end{aligned}\)

思考点二：提升采样有效性

• 不从\(P(Z)\) 中sample \(Z\)
• 而从\(Q(Z)\) 中sample \(Z\)，\(Q(Z)\rightarrow P(Z|X)\)
• 然后基于\(Z\) 重建 \(\widehat{X}=f_{\theta}(Z)\)

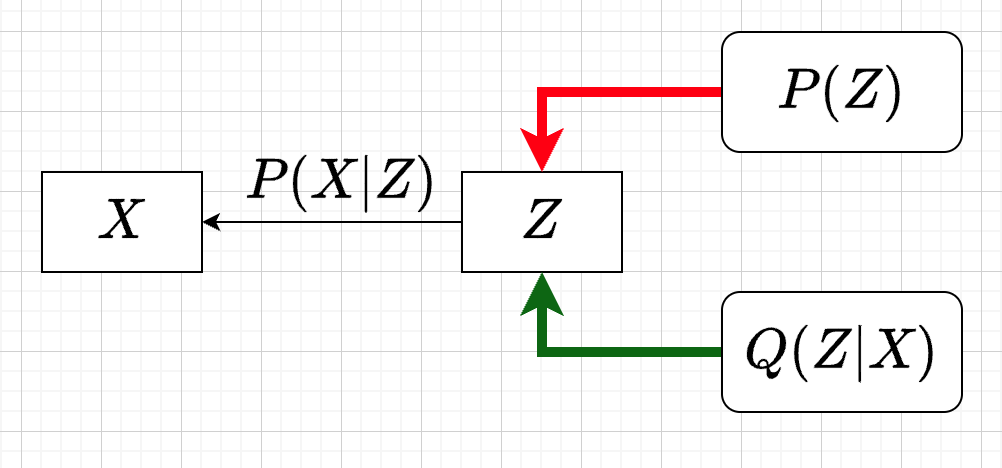
variational inference

对于任意的\(Q(Z)\)， 有

• \(\log P(X) = \mathcal{L} (Q) + \mathcal{D}(Q(Z)\|P(Z|X))\)
  • \(\mathcal{L}(Q) = E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)}\)
  • \(\mathcal{D}(Q(Z)\|P(Z|X)) = E_{Q(Z)} \log\dfrac{Q(Z)}{P(Z|X)}\)
• \(\log P(X) \ge \mathcal{L} (Q)\) ，由于 KL 非负
  • \(\mathcal{L}(Q)\) 是关于 \(Q(Z)\) 的一个泛函
  • 参数化: \(Q_{\phi}(Z)\)
  • \(\max\limits_{\phi}\mathcal{L}(Q)\) (变分的思想)
  • \(\mathcal{L} (Q)\) 就是 ELBO
• 当\(Q(Z)=P(Z|X)\) 时，\(\log P(X) = \mathcal{L}(Q)\)

证明

\(\begin{aligned} \log P(X) &= E_{Q(Z)} \log P(X) \\ &=E_{Q(Z)} \log \dfrac{P(X,Z)}{P(Z|X)} \\ &=E_{Q(Z)} \log \dfrac{P(X,Z)}{P(Z|X)} \dfrac{Q(Z)}{Q(Z)} \\ & = E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)} + E_{Q(Z)} \log \dfrac{Q(Z)}{P(Z|X)}\\ & = E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)} + \mathcal{D}[Q(Z)||P(Z|X)] \end{aligned}\)

ELBO=重建误差+正则项

• \(\mathcal{L}(Q) = \mathrm{E}_{Q(Z)}[\log P(X|Z)] - \mathcal{D}[Q(Z) \| P(Z)]\)
• 一般的，我们会让 \(Q(Z)\) 直接依赖于\(X\), 变成\(Q(Z|X)\)
• \(\mathcal{L}(Q) = \mathrm{E}_{Q(Z|X)}[\log P(X|Z)] - \mathcal{D}[Q(Z|X) \| P(Z)]\)

理解

• 第一项: reconstruction error
  • 对所有可能生成\(X\) 的\(Z\), 把似然性加权平均
  • 有了encoding,decoding的意思
    • Q(Z|X) 是对 X的一个编码
    • P(X|Z) 是对 Z的一个解码
  • 可以使用MC的方法来优化
• 第二项: 正则项
  • 需要同时最小化 Q(Z|X) 和 P(Z) 之间的距离
  • 一方面：对Q(Z|X) 做一个正则，防止 \(Q(Z|X)\) 变得过于尖锐，得到一个Dirac 分布
  • 另一方面：我们需要学习到latent space和我们要采样的空间是契合的。
• 这两项之间需要有一个balance

  • 这里我们并不希望第二项成为0，否则采样效率又降低回到从前（KL散度消失）

    如果正则项成为0，这将意味着 Q(Z|X) 不含有关于X的任何信息，隐变量失去了 他的数据表征的能力。

proof

\(\begin{aligned} \mathcal{L}(Q) & = E_{Q(Z)}\log\dfrac{P(X,Z)}{Q(Z)}\\ & = E_{Q(Z)}\log\dfrac{P(X|Z)P(Z)}{Q(Z)}\\ & = E_{Q(Z)}\log P(X|Z) + E_{Q(Z)}\log\dfrac{P(Z)}{Q(Z)}\\ & = E_{Q(Z)}\log P(X|Z) - E_{Q(Z)}\log\dfrac{Q(Z)}{P(Z)}\\ \end{aligned}\)

参数化ELBO

给定一个\(X\), \(\mathcal{L} = \mathrm{E}_{Q(Z)}[\log P(X|Z)] - \mathcal{D}[Q(Z) \| P(Z)]\)

参数化

• \(Q(Z)\) 参数化为 \(Q_{\phi}(Z|X)=\mathcal{N}(Z|\mu_{\phi}(X), \Sigma_{\phi}(X))\)
  • 每个样本对应一个z的独立的正态分布
  • \(\mu_{\phi}(X)\)，\(\Sigma_{\phi}(X)\) DNN
• \(P(X|Z)\) 参数化为 \(P_{\theta}(X|Z)=\mathcal{N}(X|f_{\theta}(Z), I)\)
  • \(f_{\theta}(Z)\) DNN
• \(P(Z)=\mathcal{N}(0,1)\)

结果

\(\mathcal{L}(\phi,\theta)=\mathrm{E}_{Q_{\phi}(Z|X))}[\log P_{\theta}(X|Z)] - \mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\) 我们有两个参数\(\phi, \theta\), \(\phi\) 出现在变分的候选函数里面，\(\theta\) 出现在decoder里面。

理解ELBO

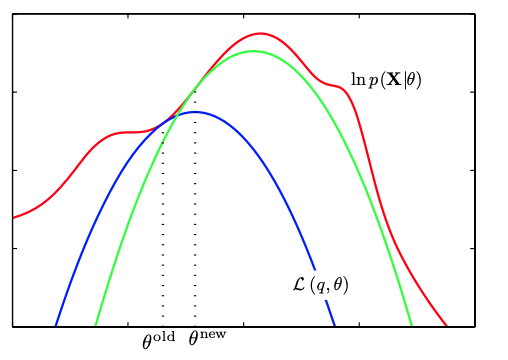
• \(\log P_{\theta}(X) = \mathcal{L}(Q, \theta) + \mathcal{D}[Q(Z)\|P(Z|X)}]\)

• 对于任意的\(Q(Z)\)，\(\log P_\theta(X)\ge \mathcal{L}(Q,\theta)\)

• 给定一个\(\theta\), \(\mathcal{L}(Q(Z), \theta)\) 是一个泛函
  • 这也是变分的意义所在，在各种函数中寻找一个最好的。
• 给定一个\(Q(Z)\), \(\mathcal{L}(Q(Z), \theta)\) 提供了一个\(\theta\) 的函数曲线
  • 不断地优化和提升下界 \(Q(Z)\)，下界成为一个代理的优化目标
  • 通过不多优化下界来更新\(\theta\)

VAE求解

\(\mathcal{L}(\phi,\theta)=\mathrm{E}_{Q_{\phi}(Z|X))}[\log P_{\theta}(X|Z)] - \mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\) 如何对\(\phi,\theta\) 求导？

• 对\(\theta\) 求导，easy
• 对\(\phi\) 求导？

对\(\phi\) 求导思路

• 第一项期望依赖的分布中有求导对应的参数, 需要重参数化
• 第二项可以显式计算，只和\(\phi\) 相关，容易计算梯度 \(\begin{aligned} &\mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\\ =& D\left[ \mathcal{N}(\mu_{\phi}(X), \Sigma_{\phi}(X)) \parallel \mathcal{N}(0, I) \right] \\ =& \frac{1}{2} \left( \text{tr}(\Sigma_{\phi}(X)) + (\mu_{\phi}(X))^T (\mu_{\phi}(X)) - k - \log \det (\Sigma_{\phi}(X)) \right) \end{aligned}\)

重参数化

\(\nabla_{\phi} E_{Q_{\phi}(Z|X)}\log P_{\theta}(X|Z)\) ，期望依赖的分布依赖于参数\(\phi\)

• 重参数化：对随机变量做变量替换

  • before： \(Z\sim Q_{\phi}(Z|X)=\mathcal{N}(Z|\mu(X;\phi), \Sigma(X;\phi))\)
  • after： \(Z=\mu(X,\phi)+\Sigma^{1/2}(X,\phi)*\varepsilon, \quad \varepsilon \sim N(0,1)\)
  • \(E_{Q_{\phi}(Z|X)}\log P(X|Z)=E_{\varepsilon}\log P(X|\mu(X,\phi)+\Sigma^{1/2}(X,\phi)*\varepsilon))\)

• 最后期望的分布不再依赖于参数

• 求导此时可以穿过期望

  \(\begin{aligned} & \nabla_{\phi} E_{Q_{\phi}(Z|X)}\log P_{\theta}(X|Z)\\ = &\nabla_{\phi} E_{\varepsilon}\log P_{\theta}(X|\mu(X,\phi)+\Sigma^{1/2}(X,\phi)*\varepsilon) \\ = &E_{\varepsilon} \nabla_{\phi} \log P_{\theta}(X|\mu(X,\phi)+\Sigma^{1/2}(X,\phi)*\varepsilon) \end{aligned}\)

最终的求解算法

• 最后的优化目标

  \(\begin{aligned} \mathcal{L} &= \mathrm{E}_{Q_{\phi}(Z|X))}[\log P_{\theta}(X|Z)] - \mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\\ &=\mathrm{E}_{\varepsilon}[\log P_{\theta}(X|Z(\phi,\varepsilon))] - \mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\\ \end{aligned}\)

• 应用MC方法

  • sample \(\varepsilon_l \sim N(0,1), Z_l=\mu(X,\phi)+\Sigma^{1/2}(X,\phi)*\varepsilon_{l}\)
  • 计算ELBO \(\mathcal{L}(\theta, \phi, X)=\dfrac{1}{L}\sum\limits_{l=1}^{L} \log P_{\theta}(X| Z_{l})} -\mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\)
  • 对\(\phi, \theta\) 求导

前向的步骤

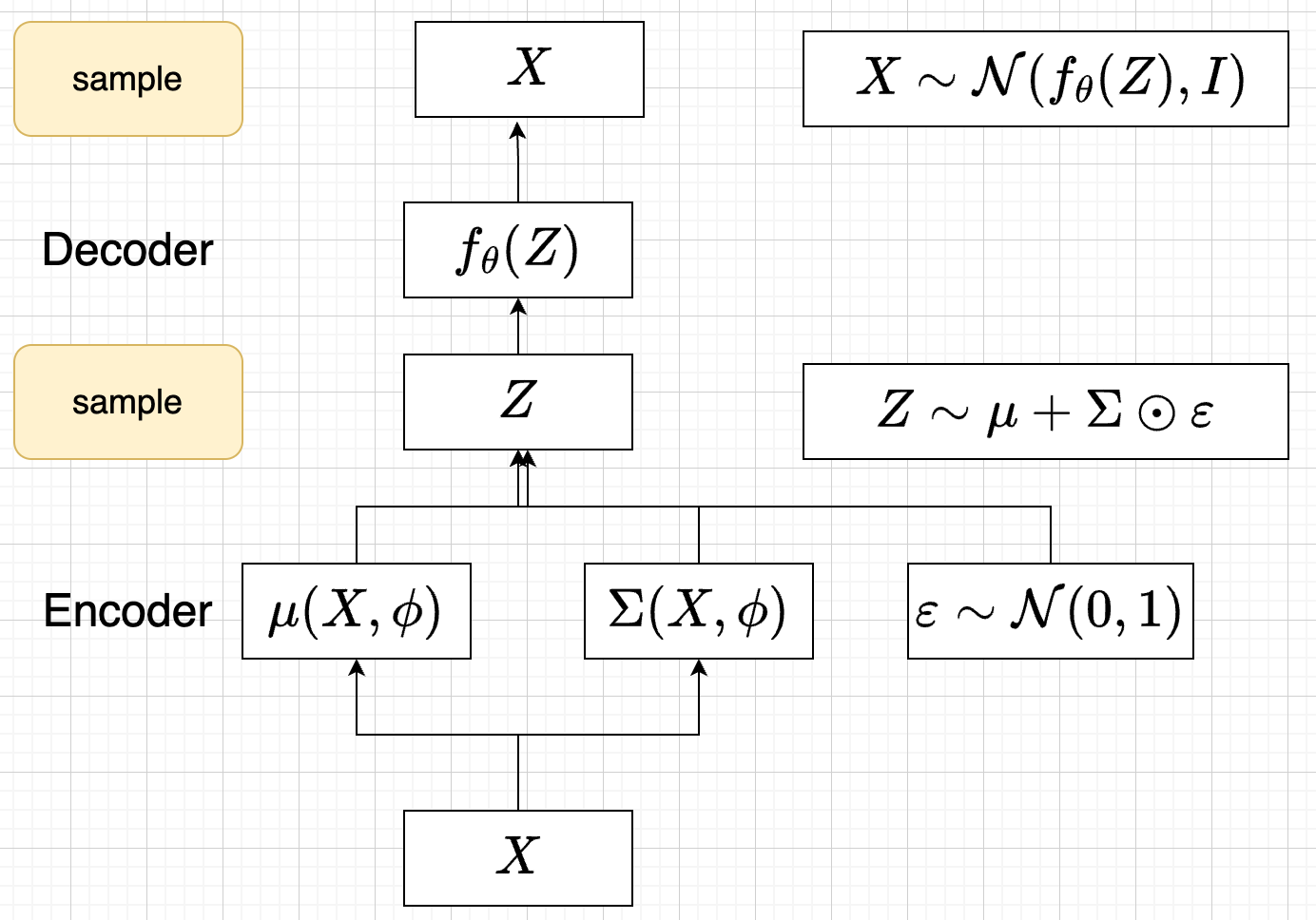
VAE训练好后怎么用？

直接生成

这个时候可以抛弃encoder \(Q(Z|X)\) 了

• sample \(Z\) from \(P(Z)\)
• 确定性函数做一个映射 \(f(Z)\)

• why？

  因为在优化的过程中 \(Q(Z|X)\) 和 \(P(Z)\) 已经比较靠近，作为优化的第二项

重构原来的图像

encoder 和decoder 都需要使用

• 基于\(Q(Z|X)\) 得到encoding \(Z\)
• 基于\(P(X|Z)\) 生成出来 \(\hat{X}\)

理论的依据

高斯分布+CDF逆变换可以拟合任意的分布

• 假设
  • 随机变量 \(N\sim \mathcal{N}[0,1]\), 对应的CDF 是\(\Psi\)
  • 那么\(Y=\Psi(N)\sim \text{Uniform}[0,1]\)
  • 目标随机变量\(X\) 对应的分布的CDF是 \(F\)
• 那么随机变量 \(X=F^{-1}(Y)\) 分布满足\(F\)

• 均匀分布+CDF逆变换可以拟合任意的分布

  • 假设

    • 随机变量 \(U\sim \text{Uniform}[0,1]\)
    • 目标随机变量对应的CDF是 \(F(x)=P(X\le x)\)

  • 结论：随机变量 \(X=F^{-1}(U)\) 分布满足\(F\)

  • 证明:

    \(P(X\le x)=P(F^{-1}(U)\le x)=P(U\le F(x))=F(x)\)

• 高斯分布到均匀分布

  • 假设
    • 随机变量 \(N\sim \mathcal{N}[0,1]\), 对应的CDF 是\(\Psi\)
    • 那么\(Y=\Psi(N)\sim \text{Uniform}[0,1]\)
  • 证明: \(P(Y\le y)=P(\Psi(N)\le y )=P(N\le \Psi^{-1}(y))=\Psi(\Psi^{-1}(y))=y\)

• 本质：

  如果能在source, target随机变量之间建立一个单调的一一映射的关系，就可以得到target 随机变量的模拟。

在生成式模型中运用：

sample \(X\) 可以分两步走

• 先sample \(Z\sim \mathcal{N}(0,1)\)
• 然后再基于一个复杂的确定函数变换（交给DNN学习）得到 \(f(Z)\) 变换得到\(X\)
• 随机变量 \(X=f(Z)\) 就是对整体的sample建模

为什么不用均匀分布做先验？而使用高斯？

• 高斯分布在整个空间上有定义，计算KL 不会有除以0的问题发生
• 高斯分布有很多很好的性质可以使用

一些思考

我们的假设：

• 可以基于隐变量来做sample
  • 先sample \(Z\), 然后基于 \(P(X|Z)\) 再sample 出来 \(X\)
• 各种高斯：
  • \(P(Z)\) gaussian，\(P(Z|X)\) ，\(P(X|Z)\) 都是gaussian， \(P(X,Z)\) 是gaussian

本质的建模：无穷个高斯模型做加权混合

• \(P(X) = \int P(X|Z)P(Z) dZ \approx \sum_{i} P(X|Z_i) P(Z_{i}) \delta Z\)
• 整体看：图像的概率分布是无穷多个高斯分布来做加权的组合
  • 且权重的分布是符合高斯分布
• 微观的看：一个图像只对应于一个高斯分布 \(\mathcal{N}(\mu(Z), \Sigma(Z))\)
  • 从生成的角度看，\(Z\) 决定和生成了\(X\)

VAE 的生成的图像模糊

• 最后的重建误差是所有像素点上的各个误差平均的结果
• 重建误差和正则项之间的balance
  • 重建误差控制了图像的质量
  • 正则项让我们向latent space的完备性上倾斜

关于噪音

• 训练的过程中出现了一次\(Z\) 的sample
• \(X\) 是基于一个不确定的，有噪音的东西生成的。
• 监督学习中也会有加入噪音的方式来训练模型，提升模型的鲁棒性，抗过拟合。

open problems

• 为什么不考虑协方差？如何建模像素之间的依赖呢？

  • 图像中最重要的一个特征是相互之间的像素的依赖性
  • 而我们的给出的假设中，\(P(Z), P(X|Z), P(Z|X)\) 统统都去掉了协方差。

• \(P(Z)\) 可以sample空间这么大，如何保证 \(P(X|Z)\) 生成出来的也是个正常的人脸？

  • 我们能把latent space 充分的学习到吗？保证它的完备性？

VAE代码实现

代码实现

model

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class VAE_Model(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        # 网络的维度是 raw_dim -> hidden_dim -> latent_dim -> hidden_dim -> raw_dim
        # encoder raw_dim -> hidden_dim -> latent_dim
        # decoder latent_dim -> hidden_dim -> raw_dim
        self.encoder_l1 = nn.Linear(raw_dim, hidden_dim)
        self.encoder_mu = nn.Linear(hidden_dim, latent_dim)  # Mean
        self.encoder_logvar = nn.Linear(hidden_dim, latent_dim)  # Log variance
        self.decoder_l1 = nn.Linear(latent_dim, hidden_dim)
        self.decoder_l2 = nn.Linear(hidden_dim, raw_dim)

    def encode(self, x):
        h = F.relu(self.encoder_l1(x))
        return self.encoder_mu(h), self.encoder_logvar(h)

    def sample_z(self, mu, logvar):
        std_var = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std_var)
        return mu + eps * std_var

    def decode(self, z):
        h = F.relu(self.decoder_l1(z))
        return torch.sigmoid(self.decoder_l2(h))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, raw_dim))
        z = self.sample_z(mu, logvar)
        return self.decode(z), mu, logvar

loss

1
2
3
4
5
6
7

# Model, Optimizer, and Loss Function
def loss_function(recon_x, x, mu, logvar):
    # 计算重建的误差，只和recon_x, x 有关
    RECON = F.mse_loss(recon_x, x.view(-1, raw_dim), reduction='sum')
    # 计算KL散度 D(P(Z|X)||Q(Z)) 只和 mu, logvar 有关
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return RECON + KLD

train

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def train():
    model = VAE_Model().to(device)
    model.train()
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        x = data.to(device)
        optimizer.zero_grad()
        recon_x, mu, logvar = model(x)
        loss = loss_function(recon_x, x, mu, logvar)
        loss.backward()
        train_loss += loss.item()
        optimizer.step()

总结

生成模型

• 概率建模 \(P(X)\)
  • 目的是为了采样，生成样本以外的x
  • 计算似然性
• 如果直接基于autoregressive model，decode代价太大
• 基于隐变量的方式: \(Z\rightarrow X\)

求解：

• 每个X的背后都有一个Z，但是Z未知，所以需要遍历Z \(P(X)=\int P(Z)P(X|Z) dZ\)
  • log 很难处理
  • 很难采样到对X有实质贡献的Z
• Jensen 不等式得到了似然函数的变分下界
  • 最大似然转化为了对下界的优化上
  • \(\log P(X) \ge \mathcal{L} (Q)\)
  • \(\mathcal{L}(Q) = E_{Q(Z)} \log \dfrac{P(X,Z)}{Q(Z)}\)
• 优化下界： \(\mathcal{L}(\phi,\theta)=\mathrm{E}_{Q_{\phi}(Z|X))}[\log P_{\theta}(X|Z)] - \mathcal{D}[Q_{\phi}(Z|X) \|P(Z)]\)
  • 下界中有两套参数 \(\phi, \theta\)
  • 变分相关的参数 \(\phi\), encoder, 不断地提升下界
  • 似然函数中的\(\theta\), decoder

使用：

• 使用的时候我们会丢掉 Encoder, 使用Decoder

优化中的独特点：

• 对下界来优化
• 有两套参数：一个是优化提升下界的，一个是正常的参数

建模的本质：无穷个高斯和一个高斯

对于一个图像\(X\)

• 如果Z不知道的情况下，X是无穷个高斯分布的组合 \(P(X)=\int P(Z)P(X|Z) dZ\)
• 当Z知道的情况下，X只对应唯一一个高斯分布\(\mathcal{N}(\mu(Z), \Sigma(Z))\)

参考论文