解密旋转位置编码

背景

主要内容

• 旋转位置编码在大模型中应用广泛
  • meta llama
  • google PaLM
  • xAI Grok
• 内容
  • 旋转位置编码的来龙去脉
    • 基于实数域上的旋转变换来推演
    • 代码实现
  • 理解 sinusoidal positional encoding
• 参考：
  • 2021. Enhanced Transformer with Rotary Position Embedding (Su et al. 2022)
  • 2017. Attention Is All You Need (Vaswani et al. 2023)
  • hugging face llama

题外话

• 系列讲座会偏数学

• 周鸿祎驳斥“程序员将不再存在”言论

  最近我唯一后悔的事情是我大学期间没有认真学线性代数，当时没有人告诉我线性代数有什么用， 我也想不通为什么一个个矩阵乘来乘去有什么用。过来二三十年后我才发现，原来线性代数藏在 大模型的并行计算里面。所以，AI时代来临意味着更多计算机人才，数学人才的缺口。

回顾transformer

• encoder: 寻找算子\(\mathcal{T}\) 低阶语义向量序列转化为高阶的语义向量序列

  \(\mathcal{T}\begin{pmatrix} X_1\\ X_2\\ \vdots\\ X_N \end{pmatrix} \rightarrow\begin{pmatrix} Y_1\\ Y_2\\ \vdots\\ Y_N \end{pmatrix}\)

• \(Y=\mathcal{T}(X)=\mathcal{F}(\mathcal{A}(X))\)

  • Attention \(\mathcal{A}\)
  • Feedforward \(\mathcal{F}\)

• Attention

  \(\begin{aligned}Q_{i} &= X_{i} W_{Q} \\ K_{i} &= X_{i} W_{K}\\ V_{i} &= X_{i} W_{V}\\ Y_{i} &= \sum_{j=1}^{N}sim(Q_i,K_{j}) V_j\\ sim(Q_{i},K_j) = &= \frac{exp(\frac{Q_{i}K_{j}^{T}}{\sqrt{D}})} {\sum_{j=1}^N exp(\frac{Q_iK_j^{T}}{\sqrt{D}})}\\ \end{aligned}\)

为什么需要位置编码

• 因为transformer结构本身是和位置无关的 \(Y=\mathcal{T}(X)=\mathcal{F}(\mathcal{A}(X))\)
• 高阶语义向量不仅仅是由周围token的语义向量组合表达而成
  • 还需要加上每个token所处的位置
• 下面的cls token得到的语义向量是完全一样的。
  • <cls> 从 北京 到 上海 的 火车票
  • <cls> 从 上海 到 北京 的 火车票
• 其他的网络结构天然有序列的位置信息 RNN/CNN

如何加入位置编码

\(\mathcal{T}(X)=\mathcal{F}(\mathcal{A}(X))\)

• \(\mathcal{F}\) 是位置无关的
• 可以修改 \(X\) 或者 \(\mathcal{A}\)

直接修改输入

在\(X_i \rightarrow Q_i, K_i, V_i\) 之前，直接加入位置的embedding \(X_i^{’}=X_i+P_i\)

learned embedding

• 优点简单，bert/GPT
• 外推困难，对于超过序列最大长度的位置

自定义绝对位置编码

• 二维函数 f(position, dimension)

• 要求

  • 函数随着position,dimension增长应该是有界的
  • 足够的区分度，对每个position,对应的行向量应该是不同的

• 例子

  \(\begin{aligned} P_{i,2t} &= sin(k/10000^{2t/D}) &&\\ P_{i,2t+1} &= cos(k/10000^{2t/D})&&\\ \end{aligned}\)

  \(t\in[0,1,\ldots,D/2-1], i\ge0\)

• 问题: 语义应该是和相对位置有关的，而不是绝对位置

修改Attention

• Attention

  \(\begin{aligned}Q_{i} &= X_{i} W_{Q} \\ K_{i} &= X_{i} W_{K}\\ V_{i} &= X_{i} W_{V}\\ Y_{i} &= \sum_{j=1}^{N}sim(Q_i,K_{j}) V_j\\ sim(Q_{i},K_j) &= \frac{exp(\frac{Q_{i}K_{j}^{T}}{\sqrt{D}})} {\sum_{j=1}^N exp(\frac{Q_iK_j^{T}}{\sqrt{D}})}\\ \end{aligned}\)

• 想法

  • 从相似性入手：i和j之间的语义的相似性应该包含相对的距离信息
  • \(Q_{i}K_j^T=g(X_{i},X_j,i-j)\)

回顾矩阵的知识

关于行向量和矩阵

• 定义线性算子 \(\mathcal{A}\)

  • 可以作用到行向量 \(\mathcal{A}(X_i) = X_{i} A\)
  • 也可以作用到矩阵 \(\mathcal{A}(X) = XA\)

• 右乘矩阵等于对每个行向量逐个施加行变换

• 线性算子是对矩阵乘法的一种物理理解

  • 旋转变换

    \(R(\theta)= \begin{pmatrix} cos\theta& sin\theta\\ -sin\theta& cos\theta \end{pmatrix}\)

  • 缩放变换

    \(R(\lambda_1,\lambda_2)=\begin{pmatrix} \lambda_1 & \\ & \lambda_2 \\ \end{pmatrix}\)

• 用对角阵在正交的子空间上施加不同的行变换 假设有两个方阵A,B，设 \(X= (X^1, X^2)\), 那么

  \((X^1,X^2)\begin{pmatrix} A & 0 \\ 0 & B \end{pmatrix} = (X^1A, X^2 B)\)

• 注：

  • pytorch/tensorflow 中的矩阵相关代码都是按照行向量来组织的
  • 在ROPE 论文是按照列向量来撰写的，表现为是用矩阵左乘以一个列向量
  • 本文中出现的向量全部用行向量来表达，和代码一致

关于旋转矩阵

• 在二维子空间的旋转矩阵

  \(R(\theta)= \begin{pmatrix} cos\theta& sin\theta\\ -sin\theta& cos\theta \end{pmatrix}\)

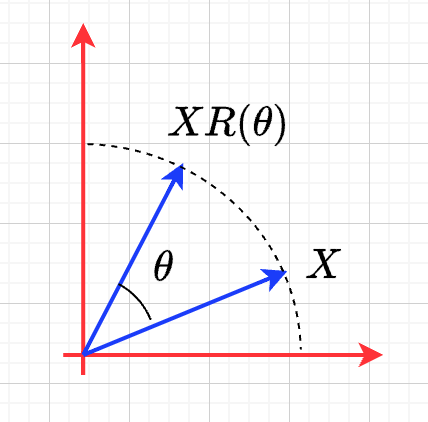
• 物理意义

  • \(XR(\theta)\) 对\(X\) 逆时针旋转\(\theta\)

  • 证明

    \(X=\rho(cos\phi, sin\phi)\)

    \(\begin{aligned} &XR(\theta)\\ =&\rho(cos \phi, sin \phi) \begin{pmatrix} cos\theta& sin\theta\\ -sin\theta& cos\theta \end{pmatrix} \\ =& \rho( cos\phi cos\theta - sin\phi sin\theta, cos\phi sin\theta + sin\phi cos\theta )\\ =& \rho(cos(\phi+\theta), sin(\phi+\theta)) \end{aligned}\)

• 性质
  • \(R(\theta)^T=R(-\theta)\)
  • \(R(\theta_1)R(\theta_2)=R(\theta_1+\theta_{2})\)

在高维空间中旋转

假设空间是偶数维的，把原始的空间切分成为一个个独立正交的二维子空间，在上面做独立的旋转。

• 定义

  \(\Theta=(\theta_{1},\theta_2,\ldots,\theta_{D/2})\)

  \(R(\Theta)=\begin{pmatrix} cos\,\theta_{1} & sin\,\theta_1 & 0 & 0 & 0 & 0 &0\\ -sin\,\theta_{1} & cos\,\theta_1 & 0 & 0 & 0 & 0 &0 \\ 0 & 0 & cos\,\theta_{2} & sin\,\theta_2 & 0 & 0 &0 \\ 0 & 0 & -sin\,\theta_{2} & cos\,\theta_2& 0 & 0 &0 \\ 0 & 0 & 0 & 0 & \ldots &0 & 0 \\ 0 & 0 & 0 & 0 &\ldots & cos\,\theta_{D/2} & sin\,\theta_{D/2} \\ 0 & 0 & 0 & 0 &\ldots & -sin\,\theta_{D/2} & cos\,\theta_{D/2} \end{pmatrix}\)

  \(R(\Theta)=\begin{pmatrix} R(\theta_{1}) & 0 &0 & 0\\ 0 & R(\theta_2) & 0 &0 \\ 0 & 0 &\ldots &0 \\ 0 & 0 & 0 &R(\theta_{D/2})\\ \end{pmatrix}\)

• 性质

  • 物理意义：在独立的二维子空间上做不同角度的旋转

    \(XR(\Theta)=(X^1, X^2) \begin{pmatrix} R(\theta_{1}) & 0 \\ 0 & R(\theta_2) \end{pmatrix}=(X^1R(\theta_1), X^2R(\theta_2))\)

  • \(R(\Theta)=\widehat{R}(\theta_1)\widehat{R}(\theta_2)\ldots\widehat{R}(\theta_{D/2})\) 逐个在不同的子空间上做旋转 定义 \(\widehat{R}(\theta_k)= \begin{pmatrix} 1 & 0 & 0 & 0 &0\\ 0 & \ddots & 0 &0 & 0\\ 0 & 0 & R(\theta_{k}) &0 & 0 \\ 0 & 0 &0 & \ddots & 0\\ 0 & 0 &0 &0 &1 \\ \end{pmatrix}\) 表示只对第k个子空间做旋转，其他子空间不动。

  \(R(\Theta)=\begin{pmatrix} R(\theta_{1}) & 0 \\ 0 & R(\theta_2) \end{pmatrix}=\begin{pmatrix} R(\theta_{1}) & 0 \\ 0 & 1 \\ \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & R(\theta_2) \end{pmatrix}=\widehat{R}(\theta_1)\widehat{R}(\theta_2)\)

旋转位置编码

motivation

• 希望
  • \(Q_{i}K_j^T=g(X_{i},X_j,i-j)\)
• 假设
  • \(Q_{i}, K_j\) 都是二维的向量，
  • \(i, j\) 是它们对应的position，这里\(\eta_{i},\eta_{j}\) 是\(Q_i, K_j\) 弧度表示.
• 基于:
  • 点积只和模长和夹角有关
  • \(Q_iK_j^T=\|Q_i\|\|K_j\| cos(\eta_{j}-\eta_i)\),
  • 如何在这里融入位置的信息？

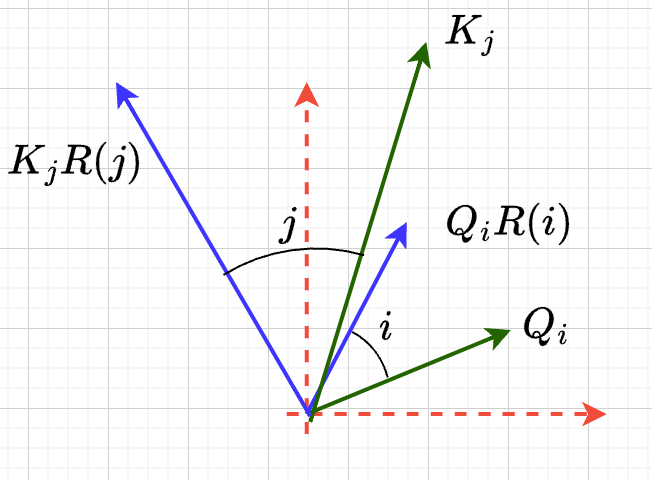
• 思路:
  • 把两个向量各自按照\(i,j\) 角度来旋转后再来计算点积
  • \(Q_iR(i)(K_jR(j))^T\)
  • 新的向量的内积带上了位置信息
• 观察新的内积:
  • 模长没有变，夹角增加了 \((j-i)\).
  • \(Q_iR(i)(K_jR(j))^T=\|Q_i\|\|K_j\| cos(\eta_{j}-\eta_{i}+(j-i))\)

二维空间中的一个解

基于旋转矩阵的一个解

\begin{equation*} \begin{split} Q_{i}&= X_{i} W_{Q} R(i\theta) \\ K_{j}&= X_j W_{K} R(j\theta)\\ Q_{i}K_j^T &=X_{i}W_QR(i\theta)R(j\theta)^{T}W_K^{T}X_{j}^T\\ &=X_{i}W_QR(i\theta)R(-j\theta)W_K^{T}X_{j}^T\\ &=X_{i}W_QR((i-j)\theta)W_K^{T}X_{j}^T\\ & =g(X_i,X_j,i-j)\\ \end{split} \end{equation*}

为什么不在投影之前做旋转？

\begin{equation*} \begin{split} Q_{i}&= X_{i} R(i\theta) W_{Q} \\ K_{j}&= X_j R(j\theta) W_{K} \\ Q_{i}K_j^T &=X_{i}R(i\theta)W_QW_KR(j\theta)^{T}X_{j}^T\\ &=?\\ \end{split} \end{equation*}

推广到高维空间

假设空间是偶数维的, 把整个空间分割成\(d=D/2\) 个子空间，在各个子空间上分别按照独立的角度来旋转

定义 \(R(i\Theta)\)

• 基础旋转角度序列 \(\Theta=(\theta_{1},\theta_2,\ldots,\theta_{d})\)
• \(i\) 位置的旋转角度序列 \(i\Theta=(i\theta_{1},i\theta_2,\ldots,i\theta_{d})\)
• \(X_{i}R(i\Theta)\) 表示对\(X_{i}\) 在各个子空间分别做角度为\(i\theta_1,i\theta_2,\ldots,i\theta_{d}\).

\(R(i\Theta)=\begin{pmatrix} cos\,i\theta_{1} & sin\,i\theta_1 & 0 & 0 & 0 & 0 &0\\ -sin\,i\theta_{1} & cos\,i\theta_1 & 0 & 0 & 0 & 0 &0 \\ 0 & 0 & cos\,i\theta_{2} & sin\,i\theta_2 & 0 & 0 &0 \\ 0 & 0 & -sin\,i\theta_{2} & cos\,i\theta_2& 0 & 0 &0 \\ 0 & 0 & 0 & 0 & \ldots &0 & 0 \\ 0 & 0 & 0 & 0 &\ldots & cos\,i\theta_{d} & sin\,i\theta_{d} \\ 0 & 0 & 0 & 0 &\ldots & -sin\,i\theta_{d} & cos\,i\theta_{d} \end{pmatrix}\)

\(R(i\Theta)=\begin{pmatrix} R(i\theta_{1}) & 0 &0 & 0\\ 0 & R(i\theta_2) & 0 &0 \\ 0 & 0 &\ldots &0 \\ 0 & 0 & 0 &R(i\theta_{d})\\ \end{pmatrix}\)

ROPE在高维空间

\begin{equation*} \begin{split} Q_{i}& = X_{i} W_{Q} R(i\Theta) \\ K_{j}& = X_j W_{K} R(j\Theta)\\ Q_{i}K_j^T &=X_{i}W_QR(i\Theta)R(j\Theta)^{T}W_K^{T}X_{j}^{T}\\ &=X_{i}W_QR(i\Theta)R(-j\Theta)W_K^{T}X_{j}^{T}\\ &=X_{i}W_QR((i-j)\Theta)W_K^{T}X_{j}^{T}\\ &=g(X_i,X_j,i-j)\\ \end{split} \end{equation*}

其中

\begin{equation*} \begin{split} R(i\Theta)R(j\Theta)^{T} &= \widehat{R}(i\theta_1)\widehat{R}(i\theta_2)\ldots\widehat{R}(i\theta_{d})\widehat{R}(j\theta_{d})^{T}\ldots \widehat{R}(j\theta_{2})^{T} \widehat{R}(j\theta_{1})^{T} \\ &= (\widehat{R}(i\theta_1)\widehat{R}(j\theta_1)^T)(\widehat{R}(i\theta_2)\widehat{R}(j\theta_2)^T)\ldots(\widehat{R}(i\theta_{d})\widehat{R}(j\theta_{d})^T)\\ &= \widehat{R}((i-j)\theta_1)\widehat{R}((i-j)\theta_2)\ldots \widehat{R}((i-j)\theta_{d})\\ &= R((i-j)\Theta)\\ \end{split} \end{equation*}

整体看下

• 空间是\(D\) 维度，\(d=D/2\)
• 有\(d\) 个正交的二维子空间 \(\mathcal{X}_1, \mathcal{X}_2, \dots, \mathcal{X}_{d}\)
• 每个子空间\(\mathcal{X}_{k}\) 有一个旋转角度基准 \(\theta_{k}\), 一个基准旋转矩阵 \(R(\theta_{k})\)
  • 合并后的基准角度序列和旋转序列是 \(\Theta, R(\Theta)\)
  • 每个子空间对应于三角函数中的一个周期 \(2\pi/\theta_{k}\)
• 对于每个位置\(i\), 角度序列和旋转序列是 \(i\Theta, R(i\Theta)\)

table

\(\begin{tabular}{|c|c|c|c|c|c|} \hline \Theta & \theta_1 & \theta_{2} & \theta_3 & \ldots & \theta_{d}\\ \hline R(\Theta) & R(\theta_1) & R(\theta_{2}) & R(\theta_3) & \ldots & R(\theta_{d})\\ \hline i\Theta & i\theta_1 & i\theta_{2} & i\theta_3 & \ldots & i\theta_{d}\\ \hline \end{tabular}\)

具体化

• \(\theta_{k}=10000^{-(k-1)/d}, k\in[1,2,\ldots,d]\)，
• 记\(B=10000^{1/d}\), 那么\(\theta_{k}=1/B^{k-1}\) 是一个等比数列
• \(B>1, k\rightarrow \infty, \theta_{k}\rightarrow 0, T\rightarrow\infty\)

\(\begin{tabular}{|c|c|c|c|c|c|} \hline \Theta & 0 & 1/B & 1/B^{2} & \ldots & 1/B^{d-1} \\ \hline T & 2\pi & 2B\pi & 2B^{2}\pi & \ldots & 2B^{d-1}\pi \\ \hline \end{tabular}\)

区分度

随着位置的增大，旋转角度是否会重复？

• 在任意第\(k\) 个子空间, 只要\(\theta_{k}\) 公式中不含有\(\pi\), 那么旋转角度序列\(\{i\theta_{k}\}_{i}\) 都不会出现周期性重复.
  • proof: 假设存在\(i,j\) 位置,使得 \(j\theta_{k}- i\theta_{k}=2m\pi\), \(m\) 是一个整数,那么 \(\theta_{k}=\dfrac{2m\pi}{j-i}\)
  • 实际中更不会重复了. 我们的定义是 \(\theta_{k} = 1/10000^{k/D}\),
• 所以在\(\theta_{k} = 1/10000^{k/D}\) 之外, 还有很多其他的选择
• 每个子空间都不会周期性重复, 整体更不会重复

可能的另外一个优势

• 在多个block 前向传递的过程中position的信息不会丢失
  • 每个block都会先做QKV的投影，然后QK投影之后会做位置旋转变换

开放性的问题

• 是否需要在这么多的子空间不断的做旋转?
• 位置编码本身维度是1
• 如果在一个二维空间里面已经可以做出区分度来了.

再看绝对位置编码

问题的定义

• 对于无穷个位置需要有个编码策略,用 D维的向量来编码
• 约束:
  • 有界性: 希望编码应该是有界的,
  • 区分度: 同时每个位置的编码应该是不同的

公式重写

\(\begin{aligned} P_{i,2k} &= sin(i/10000^{2(k-1)/D}) &&\\ P_{i,2k+1} &= cos(i/10000^{2(k-1)/D})&&\\ \end{aligned}\)

\(k\in[1,\ldots,D/2], i\ge0\)

如果记\(d=D/2,B=10000^{1/d}\)，\(\theta_{k}=1/B^{k-1}, k\in[1,2,\ldots,d]\), 第\(i\) 个位置的编码表达变成了\(d\) 个pair, \((sin(i\theta_k), cos(i\theta_k))\)

重新理解

• 有\(d\) 个正交的二维子空间 \(\mathcal{X}_1, \mathcal{X}_2, \dots, \mathcal{X}_{d}\)
• 每个子空间\(\mathcal{X}_{k}\) 有一个基础角度 \(\theta_{k}\)，
  • 两个基底, 记作\(\text{Tri}(\theta_k)=(sin(\theta_k), cos(\theta_k))\) (有界性)
  • 基础角度序列和基底序列是 \(\Theta, \text{Tri} (\Theta)\)
• 对于每个位置\(i\), 基准角度序列和基底序列是 \(i\Theta, \text{Tri}(i\Theta)\)
• 位置编码的区分度:
  • \(i\Theta\) 角度序列的独特性
  • 由 \(\theta_{k}\) 来决定各个子空间的不同
  • 子空间内部由sin,cos 来区分

• table

  \(\begin{tabular}{|c|c|c|c|c|c|} \hline \Theta & \theta_1 & \theta_{2} & \theta_3 & \ldots & \theta_{d}\\ \hline \text{Tri}(\Theta) & \text{Tri}(\theta_1) & \text{Tri}(\theta_{2}) & \text{Tri}(\theta_3) & \ldots & \text{Tri}(\theta_{d})\\ \hline i\Theta & i\theta_1 & i\theta_{2} & i\theta_3 & \ldots & i\theta_{d}\\ \hline \end{tabular}\)

• 区分度:

  随着位置的增大，位置编码会不会重复?

  • 在任意的一个子空间内, 位置编码都是唯一的,不会重复的, why?
  • proof
    • \((sin x, cos x)\) 组成的向量pair周期是 \(2\pi\)
    • 假设在第\(k\) 个子空间里面, 存在\(i,j\) 位置发生了重复,
    • 那么存在整数\(m\), 使得\(j\theta_{k}- i\theta_{k}=2m\pi\),
    • 那么 \(\theta_{k}=\dfrac{2m\pi}{j-i}\)
  • 在任意第\(k\) 个子空间, 只要\(\theta_{k}\) 公式中不含有\(\pi\), 那么旋转角度序列\(\{i\theta_{k}\}_{i}\) 都不会出现周期性重复.

• 如果我们记录 \(i=x\)

  \(\{sin(\theta_k x), cos(\theta_{k} x)\}_{k=1}^{D}\) 很像对位置函数\(f(x)\) 的一个fourier展开, \(\theta_{k}\) 对应于不同的频率

具体化

• \(\theta_{k}=10000^{-(k-1)/d}, k\in[1,2,\ldots,d]\)，
• 记\(B=10000^{1/d}\), 那么\(\theta_{k}=1/B^{k-1}\) 是一个等比数列
• \(B>1, k\rightarrow \infty, \theta_{k}\rightarrow 0, T\rightarrow\infty\)

\(\begin{tabular}{|c|c|c|c|c|c|} \hline \Theta & 0 & 1/B & 1/B^{2} & \ldots & 1/B^{d-1} \\ \hline T & 2\pi & 2B\pi & 2B^{2}\pi & \ldots & 2B^{d-1}\pi \\ \hline \end{tabular}\)

开放性的问题

• 是否需要在这么多的子空间做sin/cos,如果在一个二维空间里面已经可以做出区分度来了
• 位置编码本身维度是1

代码实现

避开旋转矩阵的相乘

why？

我们需要对每个\(Q_{i}\) 乘以不同的旋转矩阵，也就是

\(\mathcal{R}(Q)=\begin{pmatrix} Q_1 R(1\Theta)\\ Q_2 R(2\Theta)\\ \ldots \\ Q_N R(N\Theta)\\ \end{pmatrix}\)

而每个\(R(i\Theta)\) 是一个稀疏矩阵，直接matmul代价太大

在二维空间中求解

假设是二维空间，\(Q=(U,V)\), 记录

\(cos=\begin{pmatrix}cos1\theta \\ cos 2\theta\\ \ldots,\\ cos N\theta \end{pmatrix}, sin=\begin{pmatrix}sin 1\theta \\ sin 2\theta\\ \ldots,\\ sin N\theta \end{pmatrix}\)

那么

\(\begin{aligned} \mathcal{R}(U,V)&=\begin{pmatrix} u_1 cos 1\theta-v_1 sin 1\theta, u_1 sin 1\theta + v_1 cos 1\theta\\ u_2 cos 2\theta-v_2 sin 2\theta, u_2 sin 2\theta + v_2 cos 2\theta\\ \ldots\\ u_N cos N\theta-v_N sin N\theta, u_N sin N \theta + v_N cos N\theta\\ \end{pmatrix}\\ &=(U * cos - V* sin, U*sin+V*cos) \\ &= (U,V)*cos +(-V, U) *sin \end{aligned}\)

同样的，在高维空间，我们可以把\(Q\) 拆分成\(D/2\) 个列向量\(U_1,V_1,U_2,V_2,\ldots,U_{D/2},V_{D/2}\)

进一步

在各个子空间中，如果第\(k\) 个子空间\(\mathcal{X}_{d}\) 的两个列向量为\((U_{k}, V_{k})\), 我们有对应的旋转结果 \((U_{1},V_1)*cos +(-V_1, U_{1}) *sin\) \((U_{2},V_2)*cos +(-V_2, U_{2}) *sin\) \((U_{d},V_d)*cos +(-V_d, U_{d}) *sin\)

我们可以做拼接 记\(\hat{U}=(U_1, U_2, \ldots, U_d)\), \(\hat{V}=(V_1, V_2, \ldots, V_d)\) \((\hat{U},\hat{V})*cos +(-\hat{V}, \hat{U})*sin\)

code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import torch
import torch.nn as nn
import math
from torch.nn import functional as F
class Rotator:
    """根据hidden_dim，和position_ids 生成对应的旋转位置编码, 和论文中定义略有不同，一个个二维的子空间被
    分割到了前后两部分，分别进行旋转，然后拼接起来
    """
    def __init__(self, D, position_ids):
        """ position_ids: [seq_len], D 和单个头的hidden_dim对应 """
        base = 10000
        d = D / 2
        B = base ** (1/d)
        theta_base = 1.0 / (B ** (torch.arange(0, d)))    # 等比数列， $\Theta$
        thetas = position_ids.outer(theta_base)  # [seq_len, D/2]
        full_thetas = torch.cat((thetas, thetas), dim=-1)  # [seq_len, D]
        self.cos = full_thetas.cos()
        self.sin = full_thetas.sin()

    def rotate(self, x):
        """
        x: [bs, num_attention_heads, seq_len, D]
        q: [bs, num_attention_heads, seq_len, D]
        cos: [seq_len, D]
        [x,y] @ [[cos, sin], [-sin, cos]] = [x*cos-y*sin, ycos+x*sin] =[x,y]*cos+[-y, x]*sin
        """
        return x * self.cos + Rotator.reverse_half(x) * self.sin

    @staticmethod
    def reverse_half(q):
        """ q: [bs, num_attention_heads, seq_len, D] trick2 """
        u = q[..., : q.shape[-1] // 2] # 认为是各个二维子空间的第一维的向量集结
        v = q[..., q.shape[-1] // 2:]# 认为是各个二维子空间的第二维的向量集结
        return torch.cat((-v, u), dim=-1)

code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

import torch
import torch.nn as nn
import math
from torch.nn import functional as F
class Rotator:
    """根据hidden_dim，和position_ids 生成对应的旋转位置编码, 和论文中定义略有不同，一个个二维的子空间被
    分割到了前后两部分，分别进行旋转，然后拼接起来
    """
    def __init__(self, D, position_ids):
        """ position_ids: [seq_len], D 和单个头的hidden_dim对应 """
        base = 10000
        d = D / 2
        B = base ** (1/d)
        theta_base = 1.0 / (B ** (torch.arange(0, d)))    # 等比数列， $\Theta$
        thetas = position_ids.outer(theta_base)  # [seq_len, D/2]
        full_thetas = torch.cat((thetas, thetas), dim=-1)  # [seq_len, D]
        self.cos = full_thetas.cos()
        self.sin = full_thetas.sin()

    def rotate(self, x):
        """ trick1
        x: [bs, num_attention_heads, seq_len, D]
        q: [bs, num_attention_heads, seq_len, D]
        cos: [seq_len, D]
        [x,y] @ [[cos, sin], [-sin, cos]] = [x*cos-y*sin, ycos+x*sin] =[x,y]*cos+[-y, x]*sin
        """
        return x * self.cos + Rotator.reverse_half(x) * self.sin

    @staticmethod
    def reverse_half(q):
        """ q: [bs, num_attention_heads, seq_len, D] trick2 """
        u = q[..., : q.shape[-1] // 2]
        v = q[..., q.shape[-1] // 2:]
        return torch.cat((-v, u), dim=-1)


class SelfAttentionWithRoPE(nn.Module):

    def __init__(self, config):
        super().__init__()
        self.H = config["n_head"]
        self.F = config["hidden_dim"]  # F
        self.D = self.F // self.H  # D
        # 一次把qkv 全部映射完成，对应W_Q, W_K, W_V
        self.qkv_proj = nn.Linear(self.F, 3 * self.F)
        # 最后的投影，对应于 $W_O$
        self.out_proj = nn.Linear(self.F, self.F)

    def forward(self, x, position_ids):
        # position_ids: [seq_len]
        B, N, _ = x.size()
        q, k, v = self.qkv_proj(x).split(self.F, dim=-1)
        # matmul 只能在最后两个维度相乘，需要对NxD的矩阵相乘，做1,2维度的交换
        k = k.view(B, N, self.H, self.D).transpose(1, 2)
        q = q.view(B, N, self.H, self.D).transpose(1, 2)
        v = v.view(B, N, self.H, self.D).transpose(1, 2)
        # 旋转位置编码
        rotator = Rotator(self.D, position_ids)
        q = rotator.rotate(q)
        k = rotator.rotate(k)
        # 计算相似性
        att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
        att = F.softmax(att, dim=-1)
        y = att @ v
        # 多头拼接
        y = y.transpose(1, 2).contiguous().view(B, N, self.F)
        y = self.out_proj(y)
        return y


config = {"n_head": 2, "hidden_dim": 16, "batch_size": 3, "seq_len": 5}
attn = SelfAttentionWithRoPE(config)
x = torch.rand(config["batch_size"], config["seq_len"], config["hidden_dim"])
position_ids = torch.arange(config["seq_len"])
y = attn(x, position_ids)

总结

• RoPE的motivation：

  • 希望相似性只依赖于向量本身和其相对位置的距离
  • 通过对\(Q_i,K_i\) 施加 \(R(i\Theta)\) 变换做到

  \begin{equation*} \begin{split} Q_{i}& = X_{i} W_{Q} R(i\Theta) \\ K_{j}& = X_j W_{K} R(j\Theta)\\ Q_{i}K_j^T &=X_{i}W_QR(i\Theta)R(j\Theta)^{T}W_K^{T}X_{j}^{T}\\ &=X_{i}W_QR(i\Theta)R(-j\Theta)W_K^{T}X_{j}^{T}\\ &=X_{i}W_QR((i-j)\Theta)W_K^{T}X_{j}^{T}\\ &=g(X_i,X_j,i-j)\\ \end{split} \end{equation*}

• RoPE是什么？

  \(\begin{tabular}{|c|c|c|c|c|c|} \hline \Theta & \theta_1 & \theta_{2} & \theta_3 & \ldots & \theta_{d}\\ \hline R(\Theta) & R(\theta_1) & R(\theta_{2}) & R(\theta_3) & \ldots & R(\theta_{d})\\ \hline i\Theta & i\theta_1 & i\theta_{2} & i\theta_3 & \ldots & i\theta_{d}\\ \hline \end{tabular}\)

  • 把原空间切分成为一个个正交的二维子空间，在上面做独立的旋转。
  • 在每个子空间上角度不会发生周期性重复

• 绝对位置编码和RoPE 有相似的结构

  • 在每个子空间上编码都不会发生周期性重复

参考论文